【編者注:本文摘錄自系列短文,該系列文章基於亞斯敏·馬赫納茲·法魯基博士(Yasmeen Mahnaz Faruqi)博士發表于《國際教育雜誌》(International Education Journal)的論文《伊斯蘭學者對科學事業的貢獻》。】
8世紀至13世紀間,伊斯蘭世界的數學科學蓬勃發展。學者們在繼承希臘、印度、巴比倫和波斯數學傳統的基礎上,提出了大量新的理論與方法。穆斯林學者採納了印度數位體系,並引入了“零”(sifr)的概念,從而改進了算數運算。這一變革極大地改變了計算方式,並通過安達盧斯地區(今西班牙、義大利和葡萄牙的部分地區)傳入歐洲。
被譽為“代數之父”的花拉子模(al-Khwarizmi)奠定了現代代數學的基礎;十一世紀穆斯林數學家、天文學家歐麥爾·赫亞姆(Umar Khayyam)推進了三次方程的研究;中世紀伊斯蘭黃金時代最傑出的天文學家和數學家阿爾·白塔尼(al-Battani)發展了三角學,對天文學和航海產生了深遠影響。博學家伊本·海賽姆(Ibn al-Haytham,拉丁文名 Alhazen)在光學、幾何學和實驗科學領域作出了重要貢獻,其著作後來啟發了開普勒和培根等歐洲學者。通過將代數與幾何相結合、引入新的數論研究並發展數學建模方法,伊斯蘭數學家不僅保存了古代數學知識,還在此基礎上進一步推進了數學、科學與探索活動的發展,對伊斯蘭世界以及文藝復興時期的歐洲產生了深遠影響。
圖1. 花拉子模環形山(維琪百科);圖2. 阿爾·白塔尼(Albategnius)環形山(維琪百科);圖3. 伊本·海賽姆(Alhazen)環形山(維琪百科);圖4. 歐麥爾·赫亞姆環形山(維琪百科);圖5.(環形山下方圖片)“三兄弟”——長兄穆罕默德(Mohammed)、次兄艾哈邁德(Ahmed)和幼弟哈桑(Hasan)——以“巴努·穆薩”(Banu Musa)之名撰寫了20餘部科學著作(newarab.com)
在這一時期,伊斯蘭世界的數學科學實踐涵蓋了數學、代數和幾何,同時也包括數學地理、天文學和光學。穆斯林在算術領域形成的數論(‘ilm al-a‘dad)主要源自希臘數學文獻的翻譯成果,例如歐幾裡得《幾何原本》第七至第九卷,以及傑拉什的尼科馬庫斯所著的《算術入門》(Berggren,1997)。
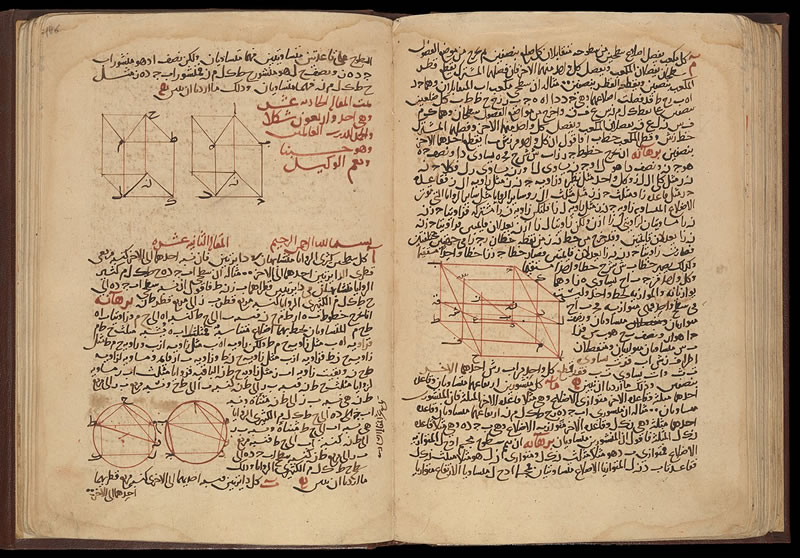
圖6. 伊斯哈格·伊本·胡納因(Ishaq Ibn Hunayn)翻譯的歐幾裡得《幾何原本》阿拉伯文譯本,推測作於伊拉克巴格達,西元1270年(伊曆699年)。藏於賈斯特·比蒂圖書館 。伊斯哈格·伊本·胡納因(約830年—約910/911年)是著名翻譯家胡納因·伊本·伊斯哈格之子,也是一位傑出的阿拉伯醫生和學者。他撰寫了第一部阿拉伯語醫師傳記,並因翻譯歐幾裡得的《幾何原本》和托勒密的《天文學大成》而聞名,這些譯作在希臘科學向伊斯蘭世界及中世紀歐洲的傳播過程中發揮了關鍵作用。(維琪百科)
此外,穆斯林學者從印度(印度教文化),甚至可能從中國引入了數字體系,並推動其廣泛應用。西元十世紀時,花拉子模在印度數字體系基礎之上提出了“零”(sifr)的概念,這一做法取代了繁瑣的羅馬數字體系,在數學領域引發了深刻變化,並進一步促進了行星運動預測以及天文學和地理學的發展。
伊斯蘭數學繼承了巴比倫的六十進位體系,以及印度(印度教)的十進位體系,這為數學中的數值計算方法奠定了基礎。穆斯林學者以十進位為核心發展了數學模型,用十個符號來表示所有數值,每個符號同時具有位置意義和固定數值。穆斯林數學家還發展了多種乘法運算方法,包括使用“棄九法”和小數進行驗算。因此,穆斯林學者為現代數學的發展以及數學在科學和工程領域中的應用奠定了重要基礎。
圖7. 摘自托普卡帕宮藏本,穆罕默德·庫納維(Muhammad al-Qunawi,卒於1524年)整理的阿爾·哈利利《通用輔助表》。該頁給出了函數 f(x, y)=sin y / cos x 和 g(x, y)=sin x tan y 在 x 取每一度、y 取 40°和 40°30′ 時的計算結果。(維琪百科)
阿拔斯王朝數學家、翻譯家薩比特·本·古賴(Thabit ben Qurrah)不僅翻譯了希臘數學著作,還對亞里斯多德被普遍接受的觀點提出了質疑並加以論證。在算術領域,隨著伊斯蘭數學家從非歐幾裡得的視角展開研究,無理數的概念逐漸形成。歐麥爾·赫亞姆(1048–1131)和納西爾丁·圖西(1201–1274)都對這一研究方向作出了貢獻,而這一概念並非源自希臘數學。
東部穆斯林借鑒梵文數位體系,形成了 ١、٢、٣、٤、٥、٦、٧、٨ 和 ٩ 等數位記號,並率先發展了“零”(sifr)的使用方式。西部穆斯林將零書寫為“0”,而東部穆斯林則使用符號“·”。東部穆斯林最初曾使用阿拉伯字母作為數位記號,但到九世紀時,西部穆斯林創造並採用了“古巴爾數位”(al-arqam al-ghubariyah),即1、2、3、4、5、6、7、8和9,其設計基於符號中所含角的數量來表示數值權重。零與數位體系的結合,使得通過簡潔的表達即可表示極大的數值,從而有助於解決特定數學問題。這些成果隨後通過西班牙的數學著作翻譯活動傳入歐洲。
圖8. 阿爾·凱西(Al-Kāshī)計算圓周率 π 的手稿頁面:圓周與直徑比率倍數表(jadwal tadhā’if nisbat al-muhīt wa-‘l-qutr)。(來源)
花拉子模撰寫了第一部系統性的代數學著作,“algebra”,即代數一詞,就是源自術語 al-jabr的音譯。Al-jabr指的是他在求解二次方程時所使用的兩種基本運算之一。十二世紀下半葉,花拉子模的《代數與對消還原論》(Kitab al-Jabr wa al-Muqabalah)第一部分被譯成拉丁文並在歐洲傳播。該領域的另一位重要學者是歐麥爾·赫亞姆,他對三次方程進行了系統研究,使代數逐漸被視為一門獨立的學科。此後,義大利學者繼承並拓展了他的研究方法。穆斯林學者不僅發展瞭解二次方程的技術,還編制了包含正弦、余弦、餘切等多種三角函數值的數表。阿爾·白塔尼(卒於929年)系統地發展了三角學,並將其擴展為球面三角學,這對天文學、地理學以及對已知世界之外的探索產生了重要影響,也促進了更精確地圖的繪製和對地球結構的重新認識。
圖9. 穆罕默德·伊本·穆薩·花拉子模(780–850)所著《代數與對消還原論》(Kitab fi al-Jabr wa al-Muqabala)。(互聯網檔案館)
阿拉伯幾何學不僅吸收了歐幾裡得《幾何原本》的材料和方法,還融合了阿波羅尼奧斯和阿基米德的研究成果。九世紀,阿拔斯王朝著名學者穆薩·本·沙基爾(Mūsā ibn Shākir)的三個兒子(即“巴努·穆薩”)撰寫了以阿基米德問題為基礎的《平面和球面圖形的測量》,該書通過中世紀義大利克雷莫納學者傑拉德(Gerard)的翻譯在西方廣為人知。到十七世紀,伊本·海賽姆,即阿爾哈曾,他提出的問題在歐洲被稱為“阿爾哈曾問題”,他的著作被譯成拉丁文後,使歐洲學界得以系統瞭解他在光學領域的成就,即《光學書》(Kitab al-Manazir)。書中提出了完整的視覺理論和光理論,因此他被十二世紀的學者稱為“第二托勒密”。此外,伊本·海賽姆通過強調實驗在科學研究中的作用,為現代科學方法的形成作出了重要貢獻。
圖10. 摘自巴努·穆薩所著《平面和球面圖形測量書》(Kitāb maʿrifah masāḥat al-ashkāl al-basīṭah wa-al-kuriyyah / Kitāb al-mutawassiṭāt)。(互聯網檔案館)
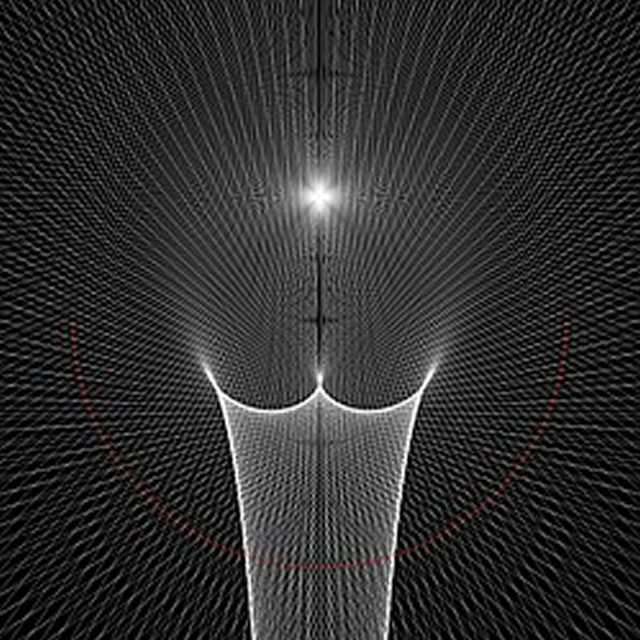
圖11. 圓形鏡面(淺紅色)內的點光源(頂部亮點)所形成的焦散線示意圖。圖中將每條光線延伸穿過鏡面成為完整直線。對於光源處的一個給定點,在焦散線暗側的第二個給定點,“阿爾哈曾問題”有兩個解,而在焦散線亮側則有四個解。(維琪百科)
伊本·海賽姆在幾何學和數論方面的貢獻遠超阿基米德傳統。他還研究了解析幾何以及代數與幾何之間聯繫的早期形態。隨後,這些研究在純數學領域促成了代數與幾何的進一步融合,其代表性成果體現在笛卡爾的幾何分析和牛頓的微積分之中。作為一位科學家,伊本·海賽姆在十世紀下半葉對數學、物理學和天文學都作出了重要貢獻。十三世紀末,英國坎特伯雷大主教約翰·佩克漢姆(John Peckham)曾參考伊本·海賽姆的《光學書》;中世紀波蘭哲學家和自然科學家威泰洛(Witelo)的《光學》同樣受到該書影響,後來又被德國數學家約翰內斯·開普勒(Johannes Kepler)所使用。英國中世紀哲學家和自然科學家,被譽為實驗科學奠基者的羅傑·培根(Roger Bacon),也極有可能使用過伊本·海賽姆的阿拉伯文原著及其拉丁文譯本。
伊斯蘭數學家在平行線理論等基礎問題上投入了大量研究,其相關定理的證明依賴于歐幾裡得公設。圍繞這些公設,穆斯林學者持續研究了五百多年,力求通過嚴格論證而非簡單接受來確立數學基礎。然而,這些研究成果在十二世紀傳入歐洲之後,直到十六世紀之前幾乎沒有得到進一步發展。總體而言,穆斯林學者不僅在數學思想與邏輯關係的構建中發揮了重要作用,還建立了一套包含“零”的有效記數體系,並由此推動了方程求解與數學建模的發展。這種將理論建構與實踐檢驗相結合的研究路徑,經由西班牙和西西里逐步傳入歐洲,對近代數學及科學方法的形成產生了深遠影響。
--------------
編輯:葉哈雅
出處:Muslim Heritage
原文:Mathematical Science – Contributions of Islamic Scholars to the Scientific Enterprise
連結:https://muslimheritage.com/mathematical-science/